Small ditrigonal dodecacronic hexecontahedron

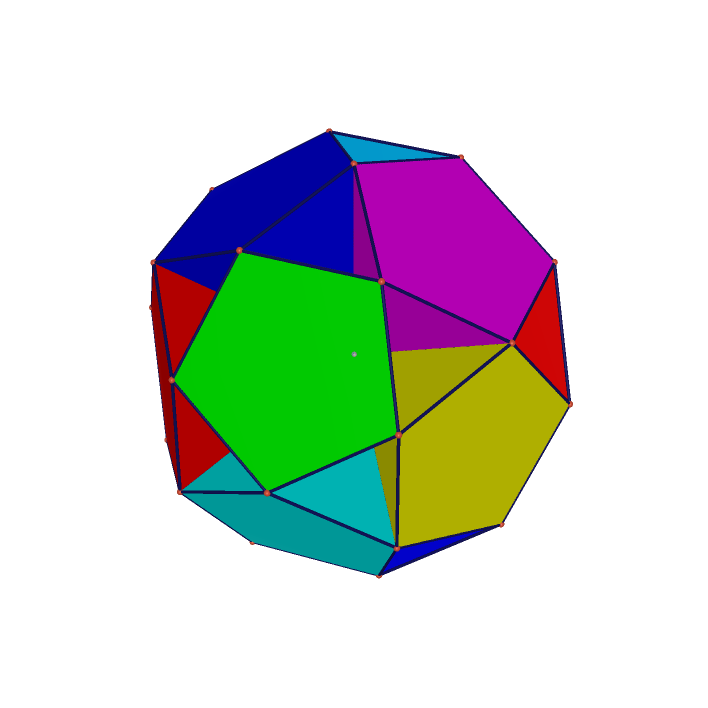
In geometry, the small ditrigonal dodecacronic hexecontahedron (or fat star) is a nonconvex isohedral polyhedron. It is the dual of the uniform small ditrigonal dodecicosidodecahedron. It is visually identical to the small dodecicosacron. Its faces are darts. A part of each dart lies inside the solid, hence is invisible in solid models.

Proportions

Faces have two angles of ${\displaystyle \arccos({\frac {5}{12}} {\frac {1}{4}}{\sqrt {5}})\approx 12.661\,078\,804\,43^{\circ }}$, one of ${\displaystyle \arccos(-{\frac {5}{12}}-{\frac {1}{60}}{\sqrt {5}})\approx 116.996\,396\,851\,70^{\circ }}$ and one of ${\displaystyle 360^{\circ }-\arccos(-{\frac {1}{12}}-{\frac {19}{60}}{\sqrt {5}})\approx 217.681\,445\,539\,45^{\circ }}$. Its dihedral angles equal ${\displaystyle \arccos({\frac {-44-3{\sqrt {5}}}{61}})\approx 146.230\,659\,755\,53^{\circ }}$. The ratio between the lengths of the long and short edges is ${\displaystyle {\frac {31 5{\sqrt {5}}}{38}}\approx 1.110\,008\,944\,41}$.

References

• Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 0730208

External links

• Weisstein, Eric W. "Small ditrigonal dodecacronic hexecontahedron". MathWorld.